
前言
在高考圆锥曲线中,我们时常可以看见以下的一个构型:
过椭圆上一点,作椭圆的两条互相垂直的弦,连接这两条弦与椭圆的第二交点,则该连线过一个定点.
例如,2020山东卷的压轴就用到了这个构型:

事实上,这个定理可以说是家喻户晓了——它就是Frégier定理.对应的,当圆锥曲线上的这一点为\(P\)时,这个定点被称为点\(P\)关于圆锥曲线的Frégier点.
那么,怎么证明这个性质呢?
当然可以用坐标方法进行证明,但是夏夏绝对不满意!事实上,二次曲线的配极才是它最本质的特征.
二次曲线配极理论的简单介绍
我们都知道点的配极(即极线(polar)):在解析几何中,它通常以切线或是切点弦的方程出现;在射影几何中,它可以表示使与过该点任作直线与圆锥曲线相交而成的两公共点分该点及此点形成调和点列的点的轨迹(这什么鬼).类似地,直线的配极(即极点(pole))也可以定义.
然而很多人不知道的是:对圆锥曲线,也可以定义配极的概念.为此,我们先介绍二阶点列这一概念[2]:
定义 成射影对应的两个线束对应直线交点的轨迹称为二阶点列.
类似地,我们也可以定义二阶线束,只不过此时的「轨迹」指这些直线所包络的图形.
然而,作出图像,很容易发现两者对应的曲线是等价的;事实上,对于非退化情形,两者均对应圆或圆锥曲线;退化的情形是平凡的.将两者放在一起看,可知两者对应的曲线都是二次曲线.
因此,我们可以想到如下定义[1]:
定义 对二次曲线 \(\omega\) 上任一点\(P\),作其关于二次曲线 \(\psi\) 的极线\(l\);当\(P\)在 \(\omega\) 上运动时,\(l\)包络一个曲线,这个曲线称为二次曲线\(\omega\)关于二次曲线\(\psi\)的极曲线(polar curve).
此外,通过对圆的情况的验证并结合射影变换,我们很容易得出定理:
定理1 二次曲线关于另一二次曲线的极曲线也是二次曲线.
关于这个定理,完整的证明可以参见[1].
特别地,如果该变换所关于的二次曲线是一个圆,我们可以得到以下结论:
特例 二次曲线关于圆的极曲线也是二次曲线;当圆的圆心在二次曲线内部时,该极曲线是椭圆;当圆心在外部时,该极曲线是双曲线;当圆心在其上时,该极曲线是抛物线.
完整的证明也可以参见[1].
此外,由定理1,我们可以得到一个简单的推论:
推论 对二次曲线上任一点,其关于另一二次曲线的极线是该二次曲线的极曲线的一条切线.
Frégier定理及其证明
现在,我们可以来构建Frégier定理了.为了叙述清晰,我们对定理进行表述:
定理(Frégier) 给定圆锥曲线 \(\omega\) 及其上一点\(P\),则对圆锥曲线上任一条弦\(AB\),若\(\angle APB=90°\),则动弦\(AB\)过定点.
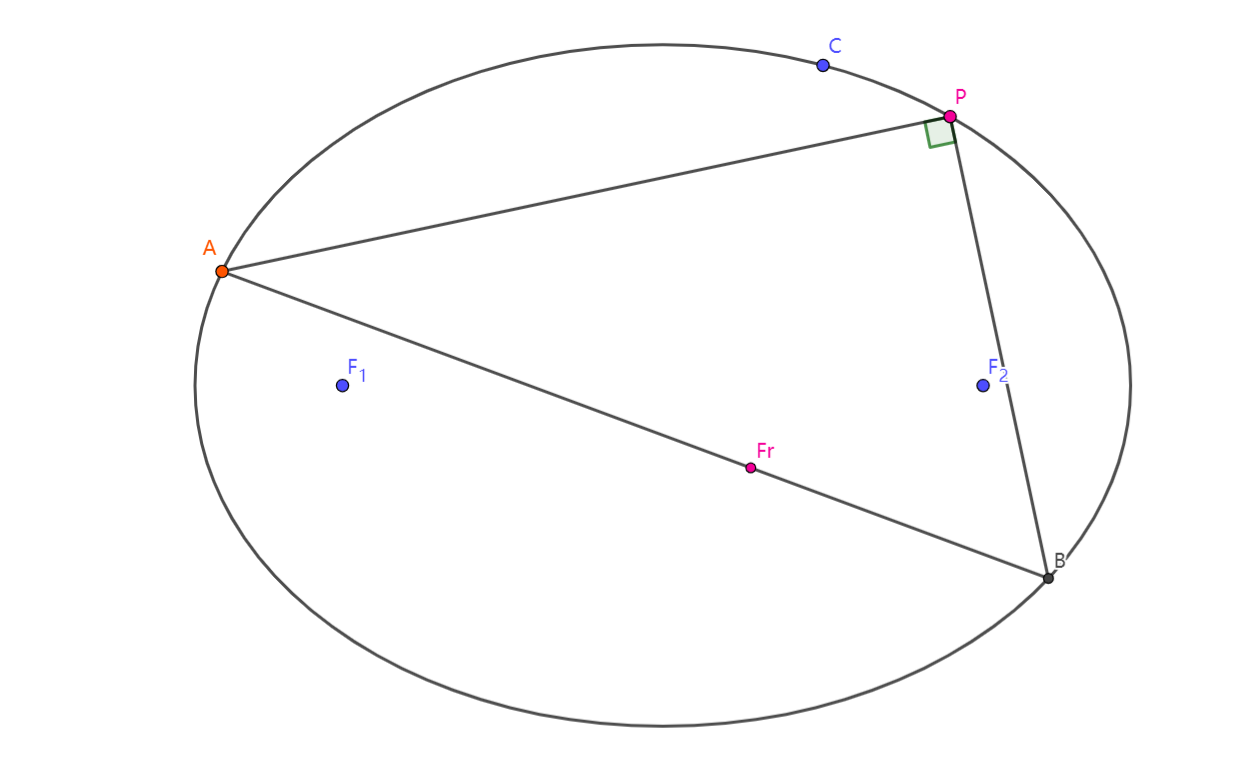
为证明该定理,我们先要引入一个引理:
引理 若抛物线的两条切线相互垂直,则这两条切线的交点在抛物线的准线上.
这不过是Monge圆在抛物线上的退化.
Frégier定理的证明 将 \(\omega\) 对以\(P\)为圆心的任一个圆配极,记配极后的图形为\(\omega'\),\(PA\mapsto A^\infty\),\(PB\mapsto B^\infty\).由定理1及其特例知\(\omega'\)也是二次曲线.
因为\(PA\)、\(PB\)过点\(P\),故\(A^\infty\)、\(B^\infty\)都是无穷远点,它们的连线是\(P\)的极线,即无穷远直线.
现在,考虑两点\(A\)、\(B\)的极线.记它们的极线是\(l_A\)、\(l_B\),由推论知\(l_A\)、\(l_B\)是抛物线\(\omega\)的切线.并且因为是关于圆的配极变换,\(\angle APB=90°\),所以\(l_A\bot l_B\).由引理,\(l_A\)与\(l_B\)的交点的轨迹是抛物线的准线.又其交点即为直线\(AB\)的极点,由La Hire定理知直线\(AB\)恒过抛物线\(\omega'\)的焦点.证毕. \(\square\)
Frégier点的轨迹、更深入的研究、展望
我们现在证明了Frégier点的存在性.那么,它的轨迹是什么呢?
由Frégier点的构造方式,我们可以看出:对抛物线上的一点\(P\),\(P\)的Frégier点其实是点\(P\)的对称直径与点\(P\)的法线的交点.具体证明这里从略啦~
于是,我们可以得到:当点\(P\)运动时,其Frégier点的轨迹应当是一条与原圆锥曲线同心且相似的一条圆锥曲线.在上面的演示中也可以看出.
然而,以上的结论并不是平凡的;也许,这可能暗示着Frégier点的另一种刻画方式?
确实如此.几个月前,夏夏曾经问过3叔叔有关Frégier点的问题,他给出的答复是运用对合线束的概念.然而这方面我还不懂(
嘛,希望以后多研究研究,先在这里留个大坑吧(逃)
后记
本篇其实是夏夏学习GOC这本书的一个笔记啦~
话说事情是这样的:当时教练给同学们测试,夏夏本来对自己的解几很有信心,结果一头栽在了Frégier点上QAQ,于是就回来恶补圆锥曲线了
(喂喂,解几和GOC这本书没什么关系吧(((
此外,还有就是尝试Zhihu on VSCode这个东西了,不得不说比知乎原生编辑器苏胡太多了,知乎你自己反省一下(不是)
就这样啦~此致
参考文献
[1] A. V. Akopyan, A. A. Zaslavsky, translated by Alex Martsinkovsky. Geometry of Conics[B]. American Mathematical Society, 2007.
[2] Sktalg.射影几何的一些东西[EB/OL].数学吧, 2016