（本文知乎版：平面几何｜浅谈平面几何中的「对称性分析」 - 知乎 (zhihu.com)）

前言

在平面几何的学习中，不知你有没有遇到过这样的问题呢？

这类问题的图形可以分为两个部分，两个部分的结构是相似的，并且在结构上的性质似乎也是相同的；至于要证的结论，则是一个同时包括两个部分中的一些点或线的命题．经过一定探索，往往可以发现这一结论可以通过两部分图形中的一些性质推出；然而这两部分图形中的性质却相互成充要条件，除去一些简单的结论，经常出现要证一边则需证另一边的情况，找不到解决问题的着力点．它就像是一种「对称」，虽然边边角角没有确切的相等关系，然而对其任意一个部分的任意一个结论，在另一边中都能找到相对应的类似结论．

那么，这一类问题有什么通性呢？又如何去解决这一类问题呢？

本文将尝试建立这一类问题的一个理论体系，并对这一类问题提出几个处理方法．在以下的内容中，我们称这一类问题为「对称性问题」，并将对此类问题的分析转为对点的分析；对于点，我们将建立一种称为「交换」的变换，并在该变换下对这类问题进行研究．

当然，本文只是本人的一个尝试，其中难免有疏漏．如有问题，还敬请各位dalao指正！

对称性问题的理论分析

（本节是理论部分，用于建立对称性问题的概念．如果只想看下面的结论的话，可以跳过本节）

现在，我们将尝试建立「对称性问题」这个概念．

众所周知：我们说一个数学对象有「对称性」，是建立在一种变换上的；任何一个对象的任一种对称性，也只能基于变换来定义及分析．例如，任何一个等边三角形在关于其轴的轴对称变换下有对称性，在关于其中心的旋转变换下也具有对称性（即所谓「旋转对称性」）．那么，「对称性问题」的对称性建立在什么变换之上呢？

本节将建立「交换」这个变换，并在此基础上给出「对称性问题」的严格定义．我们注意到，对于平面几何中常研究的直线与圆（一般二次曲线暂不纳入研究范围），都可以由多个点所确定，例如前者可由两个点唯一确定、后者可由三个点（包括广义圆）唯一确定．因此，我们主要对点的变换进行研究．这就让我们想到对点进行分类：将原几何图形中的点分为三类，即自由点、受限点和生成点．有了这样的分类，我们就能更好地进行研究．

以上内容，我们将在下面进行更为深入的阐述．

几何图形与点

我们先考虑一个问题：当我们说「研究平面几何」时，我们到底在研究什么？

有的人可能会说「我们研究的是各种各样的曲线，以及曲线与直线发生关系时产生的新的结论．」的确，在很多时候，我们研究的确实也是如此．但这并没有很好地回答我们的问题：当我们说「研究平面几何」时，我们到底在研究什么？

这就引出所谓的「轨迹」概念：平面上，在一定的限制条件下可取的点构成的集合，因此，所有的曲线，其本质都是点的轨迹．

那么，这对我们的研究有什么帮助呢？很遗憾，帮助并不是很大……但这个概念给我们带来了一个研究思路：即从对图形中一般几何对象的分析，转为对图形中的点的分析．

如何进行呢？事实上，我们可以从决定曲线形状的点入手．

我们都知道：一条直线由两个点（端点）唯一确定，一个圆由不共线三点唯一确定．因此，对一个几何对象的研究，可以转为对确定其位置及形状的点进行研究．因此，由于一个完整的几何图形是由多个几何对象组成的，有关整个几何图形的研究，也就可以看作对决定了图形的点进行研究．

举个例子，在下面这张图（2019联赛A卷二试1）中，虽然可以看见许多的线与圆，但决定这些元素的是图中的点：点$A, B, C$决定了三角形$ABC$及中点$M$，点$P$决定了两个圆，又和$MP$一起决定了$D$和$E$．因此，要研究这个图形，我们只需要研究其中的点即可．

但是，由上面的分析，我们发现：一些点是由另一些点决定的，有关这些点的分析，本质上是对决定它们的点进行分析．因此，我们应该怎样去分析这些点呢？

自由点、受限点与生成点

从上面的例子中，我们已经看到这些点之间的依赖关系：一些点可以自由移动，另一些点则由前一种点的位置确定，后面的点是被前面的点唯一确定的．为此，我们提出三个概念：「自由点」、「受限点」和「生成点」．

定义1 如果一个点的位置不由其它的点唯一确定（也就是说，这个点可以自由移动），则称这个点为自由点．

定义2 如果一个点的位置不由其它的点唯一确定，但它的轨迹由其它的点唯一确定，则称这个点为「受限点」．

定义3 如果一个点的位置由其它的点唯一确定，则称这个点为生成点．

生成点为什么叫「生成点」？我们观察上面的图形．在上面的图形中，中点$M$是由限制条件「线段$BC$的中点」唯一确定的，因此可以说「这个点是从自由点$P$、$Q$生成的．」同理，观察点$D$，它是由限制条件「直线$PM$与圆$APB$的交点」唯一确定的，因此可以说「这个点是从点（不一定要是自由点）$A$、$B$、$P$、$M$生成的」．由此，读者不难推致「生成点」的起名原因了．

判断一个点的类型的简单方法：将这个图用geogebra作出来，如果给出的点是深蓝色，那它就是自由点；如果是浅蓝色就是受限点；如果是黑色，那就是生成点啦www

一种变换：「交换」

下面，我们可以进入正题了：所谓「对称性问题」的理论分析．但在那之前，我们先要明确：「对称性问题」到底是关于什么对称的？

为此，我们需要更仔细地对几何图形的结构进行研究．你可能记得，在一些讲题的文章或视频中，会出现这样的讲解：

……这两个点的地位是相同的……

好耶！这似乎就是所谓「对称性」所在了．但是，什么叫「地位相同」？？？

为了解决这个问题，我们尝试从几何图形的结构入手．例如，在下面这张图（2019CMO部分图形）中，你看到了什么？

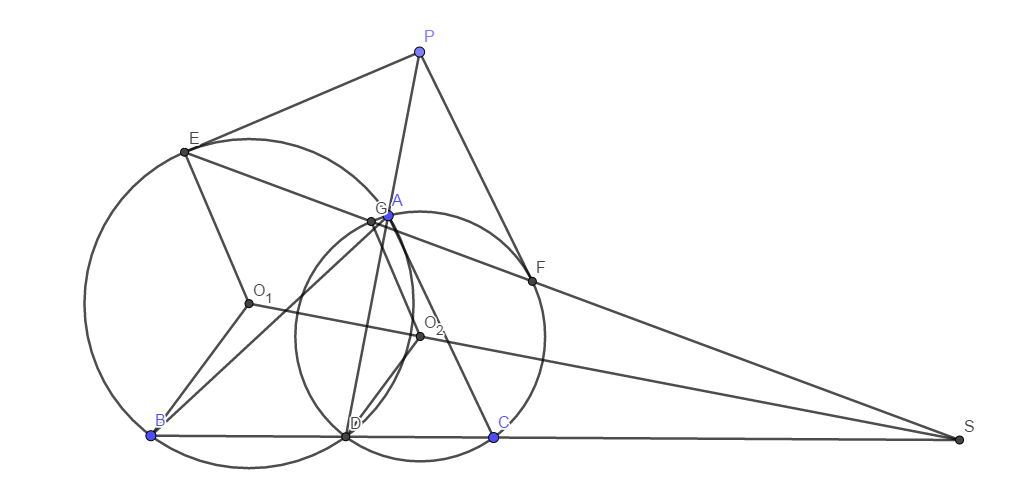
在这张图中，$AD$是角平分线，$S$是两圆的外位似中心，$P$是两圆根轴上一点，$PE$、$PF$是切线．于是，在这张图中，圆$ABD$、圆$ACD$「地位是平等的」，点$E$、$F$「地位是平等的」．在这里是什么意思？

事实上，如果我们仔细观察这个结构，可以发现一些相似的结论：

$O_1F\bot PE$，$O_2F\bot PF$；
$O_1B=O_1D=O_1A$，$O_2C=O_2D=O_2A$；
……

在这里，我们可以发现：对于这些结构，其对应的结论也是相似的．另外，如果把两边一起看，又会有一些新的结论：

$EBCF$四点共圆；
$PE=PF$；
……

在这里，我们又能发现什么？

综合上面的两组结论，我们可以发现：如果在上面结论中的每一条中，把$(E,F)$、$(B,C)$、$(O_1,O_2)$分别互换，所得的新结论与圆结论是相同的；对于第一组，把前一个结论如此替换后就变成后一个结论；对于第二组，结论在互换前后不变．这里又体现出了一种对称性：在结构对称的图形中，其每个结构中的对应结论在点的互换意义下也是对称的．

更进一步：如果把对称点中的自由点和生成点分开，对两类点分别考虑，会发生什么呢？

由于生成点是由自由点唯一确定的，因此，如果把两个自由点互换，它们对应的受限点、生成点、结构等也会互换．基于此，我们就可以提出一种新的变换：

定义4（交换变换） 对于一个图形$g$，定义一种变换：$g'=\epsilon(g,A,B)$．它的意义是对图形$g$中的两个自由点$A$、$B$，将这两个点互换（因此由这两个点所决定的几何元素也一起互换了），得到一个新图形$g'$．

在这个角度下，我们就可以定义所谓对称性了：

定义5（对称性） 对于一个图形$g$及其中的两个自由点$A$、$B$，若$\epsilon(g,A,B)=g$，则称图形$g$关于自由点$A$、$B$具有对称性．

结合之前的探索，我们知道，如果点对称，它们对应的结论也是对称的．从这个角度，我们可以对「结论」也作一个「对称性」的定义．这里就从略了，请读者自行思考，这一定义应该是怎样的呢？

「变」与「不变」

我们再来看之前那个例子．

我们现在可以看出，原图关于自由点$(B,C)$具有对称性：将$B$与$C$互换，则圆$O_1$与圆$O_2$互换，$E$与$F$也互换，原图中所有与$B$或$C$有关结构与结论都互换了，然而互换后原图的结构是不变的（点$G$看似没有对应点，其实只是没有画出来）．那么，问题是：在这个变换下，哪些东西变了（形式上的），哪些东西没变？

我们先从几何结构开始吧．

首先，与$B$、$C$有关的点肯定互换了，于是一个点没有发生变化，它一定与$B$及$C$无关，或者是同时由$B$和$C$共同决定的点．

对于前者，有哪些呢？

首先，点$A$、$D$是不变的：点$A$是自由点，点$D$是由$A$、$B$、$C$共同确定的生成点．因此，根轴$AD$是不变的．

其次，对根轴$AD$，其上的点$P$是受限点，它受到点$A$、$D$的限制．因此，$P$在此变换下也是不变的．

点$S$呢？我们发现，它是$EF$与$BC$的交点，又是圆$O_1$与圆$O_2$的外位似中心．因此，它同时与$B$ 、$C$有关，当然是不变的啦．

对于这样在变换下不变的元素，我们称这样的元素为「不变元素」．如果一个不变元素是点，则称它为「不动点」．

对于后者呢？还记得上面说的第一组结论、第二组结论吗？

事实上，如果我们仔细观察这个结构，可以发现一些相似的结论：

$O_1F\bot PE$，$O_2F\bot PF$；

$O_1B=O_1D=O_1A$，$O_2C=O_2D=O_2A$；

……

在这里，我们可以发现：对于这些结构，其对应的结论也是相似的．另外，如果把两边一起看，又会有一些新的结论：

$EBCF$四点共圆；

$PE=PF$；

……

在这里，我们又能发现什么？

对于第一组，结论在点互换后也是互换的；但让我们感兴趣的是第二组．对于第二组结论，它们自身在互换前后是不变的．我们把这样的结论称为「不变结论」．

不变结论与不变元素统称为「不变量」．

现在，我们就可以对「对称性问题」下一个定义了：

定义6 如果关于图形$g$的平面几何问题，其中图形$g$关于其中两点具有对称性，且其欲证结论为关于这两点的不变结论，则称这个问题为「对称性问题」．

对称性问题的处理方法

在上面，我们已经定义了「对称性问题」这一概念．那么，我们要怎样处理这类问题呢？

既然对称性问题与关于两个自由点的交换变换有关，那么，从这个变换的角度来看待就很重要了．而看待变换，最重要的无非两点：一是运用不变量，二是对变换中性质的打破．

运用不变量

对对称类问题，这一思路的重点，即是寻找问题图形中的不变量，并尝试运用此解决问题．

例1（初二难度）

如图，点$B$、$A$、$C$按顺序排列在一条直线上，在直线的同向作等边三角形$ABD$、$ACE$，连$BE$、$CD$分别交$AD$、$AE$于$F$、$G$，求证：三角形$AFG$是等边三角形．

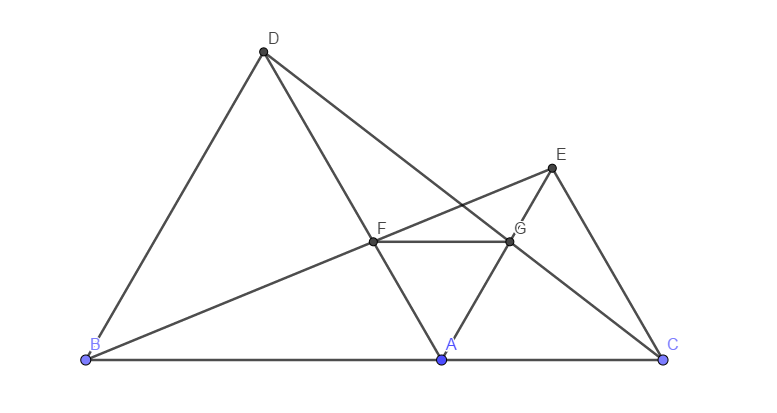
分析

例1虽然是一道初二难度的题，但它也是一道对称性问题；另一方面，它也是一道比较简单的题（知道各位都是$MOer$，当然这题是简单题啦www）为此，我们拿这道题出来，用来帮大家熟悉对称性分析．

首先我们看：哪些点是自由点、哪些点是生成点呢？

自由点和受限点——$A$是自由点，但$B$和$C$应当算自由点还是受限点呢？事实上，我们可以不拘泥于这个问题，因为当下重要的是对问题进行分析．为此，我们可以考虑把$B$、$C$当成自由点，而将$A$当成受限点．在这里，分析时要灵活考虑．

生成点——很显然了，$D$、$E$、$F$、$G$都是生成点．

再看看：哪些是不变元素呢？

交换$B$和$C$，发现所有元素都与另外的元素互换了位置，初看是没有不变元素的（除了单个的受限点$A$）．因此，我们考虑从不变性质入手．

不变性质有哪些呢？

$BE=CF$、$\triangle BAE\cong\triangle DAC$、$\triangle AFG$等边……挺多嘛，就从这里入手了！

证明

略，读者自证不难．$\square$

例2 （2012联赛）

如图，在锐角三角形$ABC$中，$AB>AC$，$M$、$N$是$BC$边上不同两点，使$\angle BAM=\angle CAN$．设$\triangle ABC$和$\triangle AMN$的外心分别为$O_1$、$O_2$，求证：$O_1$、$O_2$、$A$三点共线．

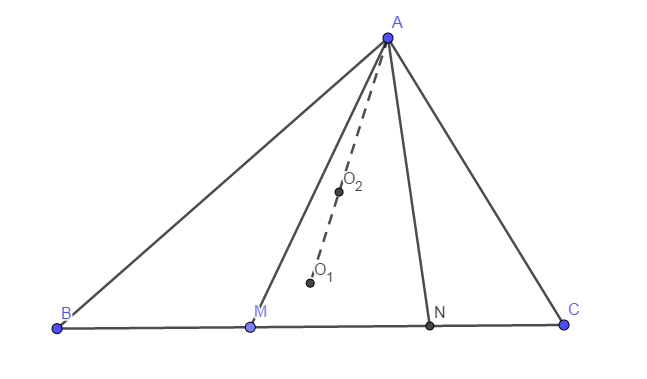
分析

本题与上题相反，同为对称性问题，但本题中，相对于$B$、$C$的不变元素更多．例如，可以很容易看出$A$、$O_1$、$O_2$都是不变元素．另一方面，$O_1$、$O_2$和$A$共线的性质正是我们要证的结论，因此直接从该不变量中考虑更好．

现在的问题是：怎么考虑呢？考虑到$O_1$、$O_2$是外心，导角肯定是一种方法；另一方面，作出两个圆，很容易发现两圆相切，我们也可以从这方面考虑．

证法1

\[ \begin{aligned} \angle BAO_1&=90°- \dfrac{1}{2}\angle AO_1B\\&=90°-\angle BCA\\&=90°-(\angle BNA-\angle NAC)\\&=90°-\dfrac{1}{2}\angle BO_2M+\angle BAM\\&=\angle BAO_2．\quad\square \end{aligned} \]

证法2

作出圆$ABC$在点$A$处的切线$l$．则 \[ \begin{aligned} \angle (AM,l)&=\angle (AB,l)+\angle MAN\\&=\angle ACB+\angle NAC\\&=\angle ANM \end{aligned} \]

故$l$为圆$AMN$切线，从而两圆相切，$O_1$、$O_2$、$A$共线．$\square$

证法3

作圆$ABC$、$AMN$，延长$AM$、$AN$交圆$ABC$于$P$、$Q$．

因为$\angle BAM=\angle CAN$，故$BP=CQ$，故$BC\parallel PQ\parallel MN$．从而$A$是$\triangle AMN$和$\triangle APQ$的顺相似中心，也是两圆的外位似中心．故两圆相切，$O_1$、$O_2$、$A$共线．$\square$

例3 （2013联赛）

如图，$AB$是圆$\omega$的一条弦，$P$为弧$AB$内一点，$E$、$F$为线段$AB$上两点，满足$AE=EF=FB$．连接$PE$、$PF$并延长，与圆$\omega$分别相交于$C$、$D$．求证：$EF\cdot CD=AC\cdot BD$．

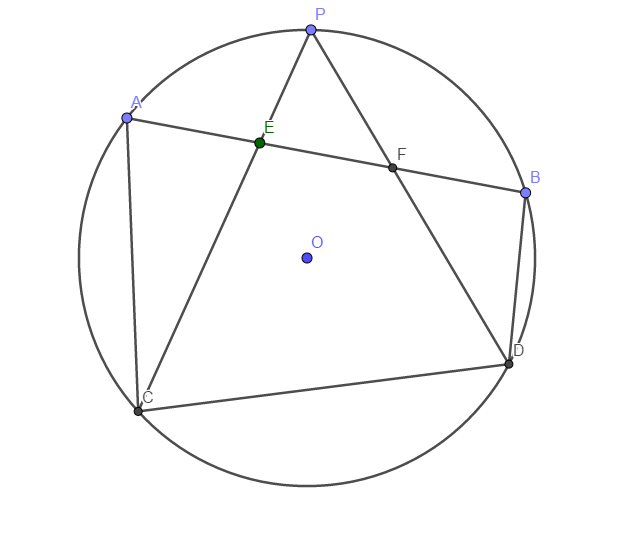
分析

我们来看一道难一点的题．可以看出，本题也是一道对称性问题（关于$A$、$B$），其中只有$P$是不动点．为此，我们来考虑不动点的问题：按理来说，对对称性问题，我们需要考虑不变元素；然而在图中我们只能找到$P$这一个不动元素．怎么办呢？

我们考虑：「构造不变量」．

回到原题．我们先来逆推分析．原题的结论相当于$AB\cdot CD=3AC\cdot BD$．观察这个结论，我们很容易想到Ptolemy定理：$AB\cdot CD+AC\cdot BD=AD\cdot BC$．如果可以证明$AD\cdot BC=4AC\cdot BD$或者$AD\cdot BC=4EF\cdot CD$该很好；可是问题是，怎么证呢？

回忆我们刚刚说过的「构造不变量」．对于「$4$」这个数字，我们想到构造两个中点——$AD$的中点和$BC$的中点．现在只需要找到一组比例就好了．而且经过探究，我们发现：$M$和$N$也是互换的．对它们的性质，有没有什么好的方法呢？

看来不动点这招是用不了了．我们来看看：不变性质上有没有突破．

证明

如图，取$AD$、$BC$的中点$M$、$N$．

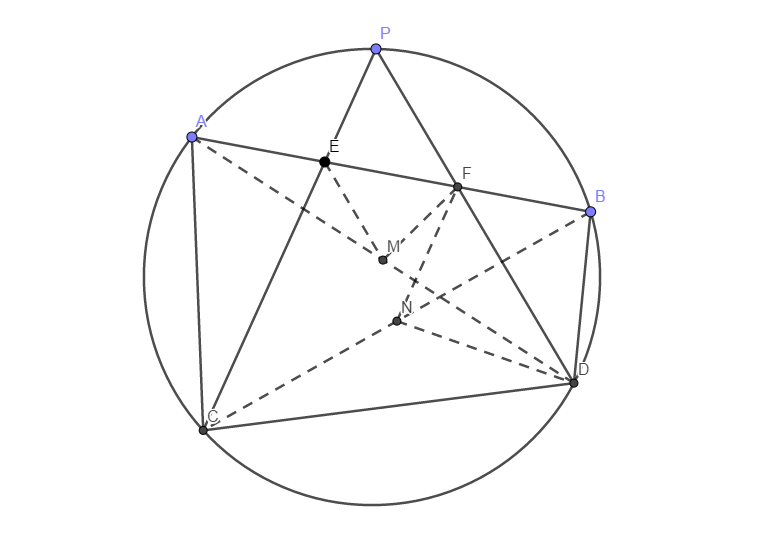
由三等分点，易知$\angle FNB=\angle ECB=\angle PDB=\angle FDB$，所以$F$、$N$、$D$、$B$四点共圆．故$\angle AEM=\angle DFA=180°-\angle DFB=180°-\angle DNB=\angle CND$．又$\angle MAE=\angle DCN$，故$\triangle MAE\sim\triangle DAN$，有$4AE\cdot CD=4CN\cdot AM=AD\cdot BC$．故$4EFCD=ADBC $．

另一方面，由Ptolemy定理，可得$AD\cdot BC=AB\cdot CD+AC\cdot BD=3EF\cdot CD+AD\cdot BC$．所以$EF\cdot CD=AC\cdot BD$，证毕！$\square$

打破对称性

以上，我们看了一些比较简单的对称性问题，并以此为例介绍了分析对称性问题的方法．然而，并非所有对称性问题都像上面的例题那样简单——很多问题的「不变元素」很难刻画，以致不得不刻画其两边对称图形的性质．除此之外，也有文章开头所讲的那样——两部分图形中的性质却相互成充要条件，除去一些简单的结论，经常出现要证一边则需证另一边的情况，找不到解决问题的着力点——的情况出现．这样一来，我们又如何解决它呢？

通过上面的分析，这一类问题的「难点」，其本质原因在于其「对称性」——证明一个结论，需要证明其对称图形的同一结论．既然如此，我们何不尝试换种角度，绕过这一「对称性」的限制呢？

「打破对称性」方法便是这一思想的一个体现．这一方法的操作如下：

明确想要在某一半图形证明的性质（这一性质通常与另一半图形的相同性质互为充要条件）；
在这一半图形中恰当地选取幻像点，使之在这一半图形中符合欲证结论；
尝试证明这一幻像点与我们需要的点是同一点．

也就是说，它的本质是「同一法」策略，尝试进行一种「非对称式」构造．可能看着不太优美，但出于解决问题的方便性，为什么不用呢？

例4 （Mannheim定理）

如图，三角形$ABC$中，一个圆同时与$AB$、$AC$和点$A$所对的弧$BC$相切，前两者的切点为$D$、$E$．求证：$\triangle ABC$的内心$I$是$DE$的中点．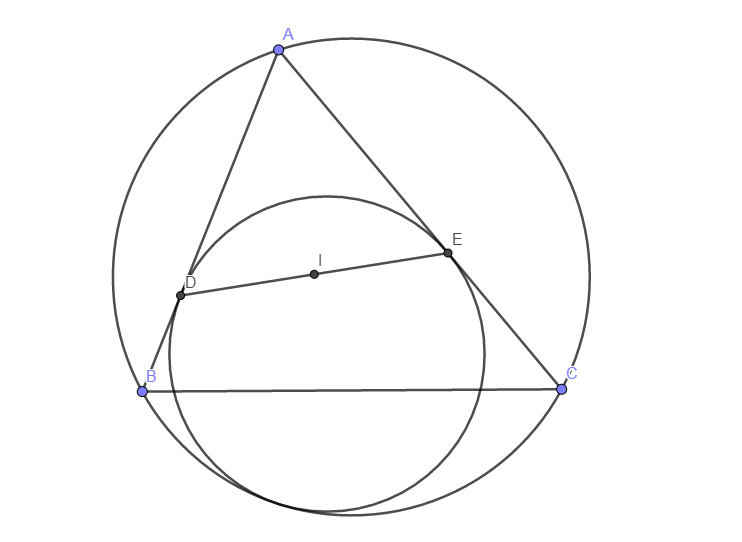

分析

我们从一个熟知的定理开始吧．这个与伪圆有关的定理，相信对于学习竞赛的你早就已经熟悉了．然而，问题是，怎么证呢？

观察图形．我们发现，原题恰好是一个对称性问题，其中$I$是不动点，它的性质也就是我们最关注的东西．另外，对于两圆相切类问题，首要的当然是做出它们的切点$T$．作出这个点，我们会发现什么呢？

——通过精确作图，我们会发现：$TIEC$、$TIDB$分别四点共圆！

我们目前不知道这一性质有何作用，因此先放一放．现在我们来顺推一下：

首先，我们看到$AB$、$AC$是切线，结合两圆相切，我们很容易想到一个熟知结论：$\angle ATE=\angle ETC$、$\angle ATD=\angle DTB$．但这一结论有没有用呢？回忆内心是三角形三条角平分线的交点，我们的直觉是——这一性质肯定有用！

现在我们假设已经证出了以上两个性质．现在看看能不能只用这两个性质导出原题——可以看出，这一方法确实可证！

于是现在，我们只需要证上面的一组共圆即可．然而，当我们在尝试时，就会尴尬地发现：证不出来……

事实是，如果要证其中的一组共圆，我们就需要一个角的关系，而导出这个角的关系恰需要另一组共圆．结合这两组共圆的地位是平等的，这一结论实际上意味着——我们要用这个共圆来证这个共圆……

死胡同了？不，换个视角，我们就能绝处逢生．

正如上面所说，证明这组共圆的主要问题是：我们需要用另一组共圆来证，因此有一个循环论证的问题．但是，我们「假装」已经证出了这组共圆，则另一组共圆也就可以证出来了．因此，如果我们从同一法角度考虑，用这组共圆来刻画这个点，先把另一组共圆推出来，最后再来证这两个点重合，不就证出了这个性质？

好耶，就这么干！

证明

用同一法．记$T$为两圆切点，设$I$为$DE$与圆$ECT$交点，延长$TE$、$TD$交圆$ABC$于$F$、$G$．

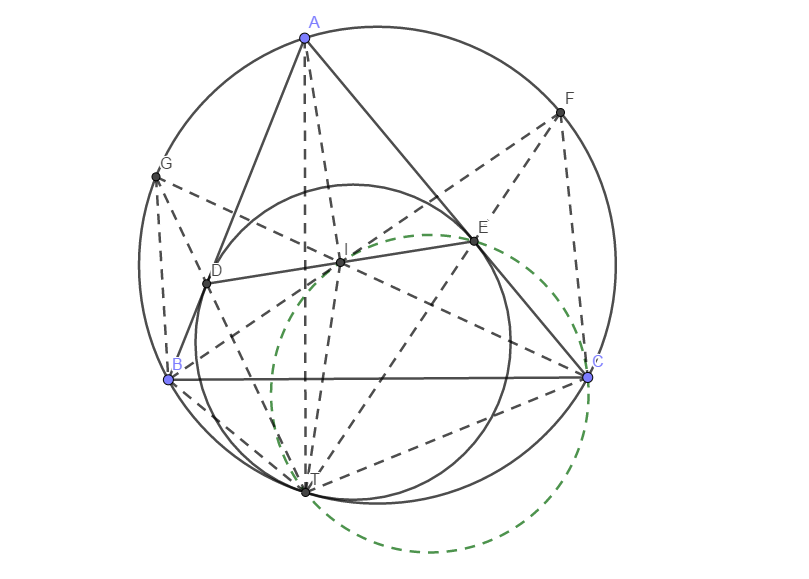
于是$\angle DIT=\angle ECT$．另一方面，由切线知$\angle TDI=\angle TEC$，故$\triangle DTI\sim\triangle ETC$，$\angle DTI=\angle ETC$．另一方面，由熟知结论知$\angle ATE=\angle CTE$，故$\angle ATE=\angle DTI$，$\angle ATD=\angle ITE$．

又由熟知结论知$\angle ATD=\angle DTB$，故$\angle BTD=\angle ITE$．结合切线知$\angle BDT=\angle TEI$，故$\triangle BTD\sim\triangle ITE$，$\angle DBT=\angle EIT$，从而$B$、$D$、$I$、$T$共圆．

现在，由于 \[ \angle ABI=\angle DTI=\angle ETC=\angle ATF=\angle ABF \]

\[ \angle ACI=\angle ETI=\angle DTB=\angle ATG=\angle ACG \]

可得$B$、$I$、$F$，$C$、$I$、$G$分别共线，很容易发现这两条直线都是角平分线．故$I$是内心，且对等腰三角形$ADE$有$ID=IE$．$\square$

分析2

当然，对于这道对称性问题，首要的还是想直接找出这个$I$的性质．如果能直接同时推出两组共线，当然最好了．可是，怎么推呢？

证明2

$F$、$G$同上．对圆内接六边形$ABFTGC$运用Pascal定理即证．$\square$

例5 （爱尖子）

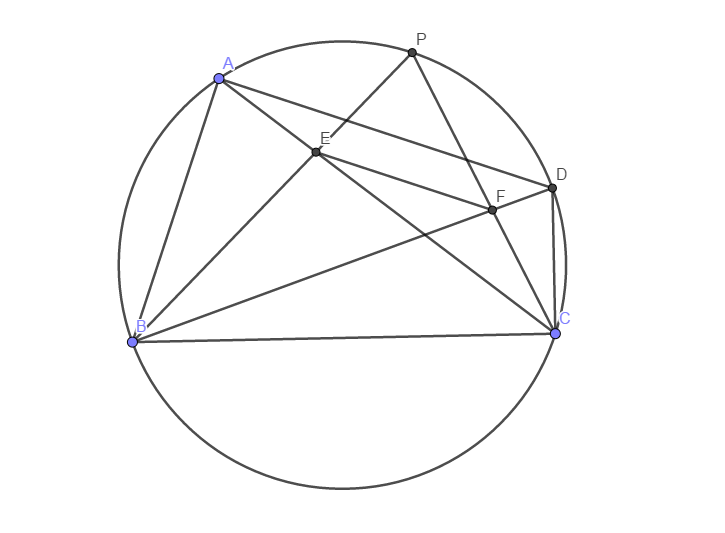
如图，四边形$ABCD$内接于圆$O$，$AB>CD$且$AB+CD=BC$．$P$为弧$AD$的中点，$PB$与$AC$交于$E$，$PC$与$BD$交于$F$．求证：$EF=AE+DF$．

分析

很容易发现该题也是一道对称性问题，唯一的不动点是$P$．问题是：$EF=AE+DF$、$BC=AB+CD$怎么用呢？

当然，对于条件，在$BC$上取点$M$使$BM=BA$似乎势在必行．对结论，在$EF$上取点$N$使$EN=EA$似乎也很显然．但是，这两个点怎么刻画呢？

——毕竟，它们是「不动点」．

我们尝试连接这两个点，发现：这根连线过$AC$与$BD$的交点！

因此，我们把这个点（就$R$吧）点出来，用$MR$定出$N$．然而推到后来，会发现也会出现一边推另一边的问题．对此，我们该怎么办呢？

证明

本题比较简单，证明我就不放了．相信看了上面的一题，你也能很快证出来！

很多问题比较复杂，需要综合运用两种技巧（「构造不变量」和「打破对称性」）．我们来看一道例题：

例6 （爱尖子）

如图，$\triangle ABC$中，$AB\neq AC$，$O$为外心，在$AB$上取点$P$使$\angle BOP=\angle ABC$，在$AC$上取点$Q$使$\angle COQ=\angle ACB$．证明：$BC$关于$PQ$的对称直线与$\triangle APQ$的外接圆相切．

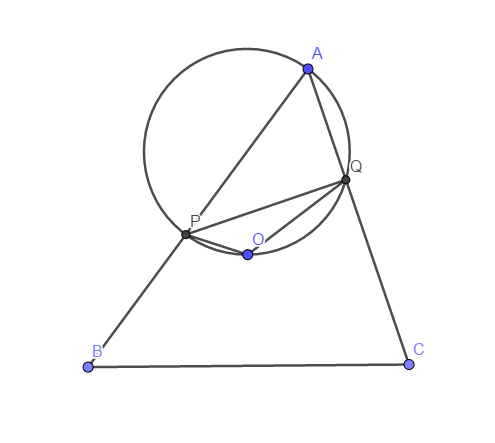
分析

本题的题设一看就不容易www

很显然本题也是对称性问题，并且不动点只有$O$，看上去是要构造不变量了．问题是，怎么构造呢？

我们还是先把题设要求的「对称直线」作出来吧，顺带切点也给作了．这就要求我们作出$PQ$与$BC$的交点：

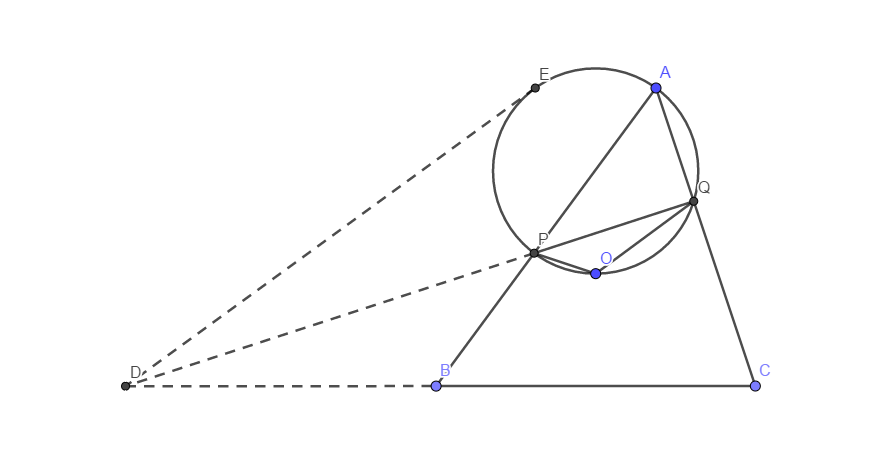
现在，我们作出了交点$D$、切点$E$．看上去这两个点都是不动点，问题是，哪个更重要？

当然是切点啦．先不管我们一开始无法说「切点」的困难，我们先来看看这个切点有什么性质．问题是，到底有什么性质呢？

我们随便拉几个圆，看看：

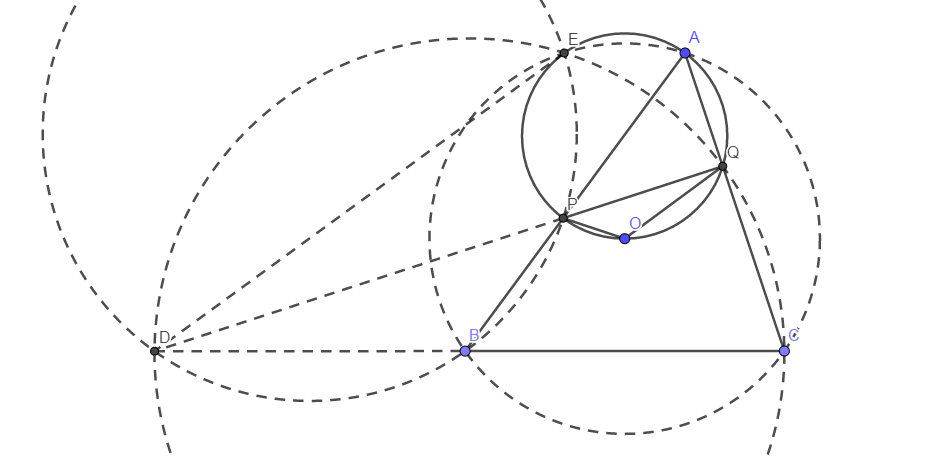
原来有这么多共圆！

由此可见，切点的性质是极其重要的了．为此，如何刻画$E$就是个问题了，圆$APQ$与圆$ABC$的交点可能可以——而且这也提示我们用到 Spiral Similarity（中文忘了，似乎是叫旋转型相似？）这个重要的性质．我们再拿尺子量一量，可以发现$QE=QC$、$PE=PB$这两个性质，事实上有了共圆这就是显然的了，所以最重要的还是那两对共圆．问题是，我们要如何推出呢？

直接推？试一下，发现不是太行，会出现像之前一样的问题（一边推另一边）．所以，我们尝试对$E$打破对称性．

来吧，上同一！

证明

如图，作$PQ$交$BC$于$D$，记圆$ABC=\Gamma$．在$\Gamma$上取一点$E$使$PE=PB$．

因为$\angle BOP=\angle ABC$， $\angle COQ=\angle ACB$，所以$\angle BOP+\angle COQ=180°-\angle BAC$．又$\angle BOC=2\angle BAC$，所以$\angle POQ=360°-(\angle POB+\angle QOC)-\angle BOC=180°-\angle BAC$，故$A$、$P$、$O$、$Q$四点共圆．记这个圆为$\Omega$．

因为$PE=PB$，$OE=OB$，所以$OP\bot BE$．又$\angle BEC=\angle BAC$，$\angle POQ=180°-\angle BAC$，所以$OP$与$BE$交点，$OQ$与$EC$交点、$E$、$O$共圆．这说明$OQ\bot EC$．

所以，$QE=QC$，有 \[ \angle QEC=\angle QCE=\angle ACE=\angle ABE=\angle BEP \] 于是$\angle PEQ=\angle BEC=\angle BAC$，故点$E$在$\Omega$上．

同时，注意到由 Spiral Similarity，有$\triangle PEQ\sim\triangle BEC$．于是$\angle EPD=180°-\angle EPQ=180°-\angle EBC=\angle EBD$，$\angle EQD=\angle EQP=\angle ECB=\angle ECD$，故$E$、$P$、$B$、$D$，$E$、$Q$、$C$、$D$分别四点共圆．于是$\angle EDQ=\angle CDQ$，即$DE$为$BC$关于$PQ$的对称直线．

由题意及对称性得：$\angle DEP=\angle PBC=\angle ABC=\angle BOP=\angle EOP$．故由弦切角定理知$DE$与$\Omega$相切．$\square$

怎么样，是不是也有想试一试的冲动？（被打

后记

以上，就是对称性问题的一些结论了，差不多就这样吧（

话说回来，这还是我第一次投出研究性的文章呢……

其实早就想写这篇文章了，大概初三时见了许多这样的一个问题，大概有了自己的一套解题思路，于是就想着写下这篇文章．可是，想了很久，最后直到高一才写出来．这篇文章写了断断续续有一个月了吧，也算费了不少时间．

后来，我与Dolphin大佬讨论了一下，感觉在「对称性」的概念这方面还有可商榷之处．Dolphin大佬提出了这样的观点：在本文中定义的「对称性」，事实上与图论中的自对应有关．对文中的「交换变换」，他也提出了很多概念，让我大开眼界．也许后面我们会合著一篇文章，探讨下这个「对称性」的本质是什么．

在这里，特别感谢Dolphin，在文章的最终定稿阶段，他帮了我许多！

另外，也感谢每一位读者，您能用心读到这里，实属不易（

既然这样……

夏夏能厚颜无耻地求个赞吗QAQ（被打

练习

完成文章中所有未给出解答的例题的证明；
证明Brocard定理：四边形$ABCD$内接于圆$O$，$AB$交$CD$于$P$，$AD$交$BC$于$Q$，$AC$交$BD$于$R$．求证：$OR\bot PQ$．
试证明Mannheim定理的两个重要推广：Thébault定理和沢山引理．
锐角$\triangle ABC$中，$AB>AC$，$P$、$Q$分别为$AB$、$AC$上的点，满足$PQ\parallel BC$，$CP$交$BQ$于$O$．$A$关于$BC$的对称点为$A'$，$A'O$交圆$APQ$于$S$．求证：圆$BSC$与圆$APQ$相切．（参考答案）
$\triangle ABC$中，$\Gamma$为其外接圆，直线$l$与$\Gamma$相切．求证：$l$关于$\triangle ABC$中各边的对称直线，两两相交形成的交点构成的三角形，其外接圆与$\Gamma$相切．（参考答案 pdf第61页）